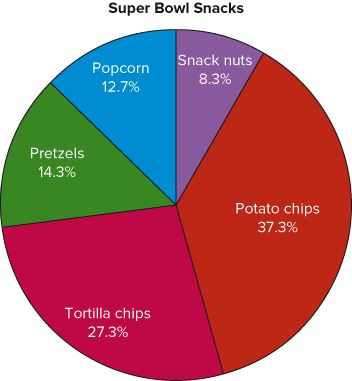
This frequency table shows the number of pounds (in the millions) of each snack food eaten during the Super Bowl.

Snack	Million Pounds (frequency)
Potato Chips	11.2
Tortilla Chips	8.2
Pretzels	4.3
Popcorn	3.8
Snack nuts	2.5
	Total (\(n\))=30.0

We need to break the circle (the pie) into different parts which represent the proportion of each class, this is (perhaps) easiest done by dividing the degrees into the parts.

---

Step 1: Split up the degrees 

\[\text{Degrees}=\frac{f}{n}\cdot 360^{\circ}\] 

Where \(f\) is the frequency for each class and \(n\) is the sum of all of the frequencies. Hence we have the following degrees split up:

Potato Chips:

\[\frac{11.2}{30}\cdot 360^\circ=134^\circ\]

Tortilla Chips:

\[\frac{8.2}{30}\cdot 360^\circ=98^\circ\]

Pretzels:

\[\frac{4.3}{30}\cdot 360^\circ=52^\circ\]

Popcorn:

\[\frac{3.8}{30}\cdot 360^\circ=46^\circ\]

Snack Nuts:

\[\frac{2.5}{30}\cdot 306^\circ=30^\circ\]

---

Step 2: For the labels the degrees don't communicate very well so use a percentage instead

Potato Chips:

\[\frac{11.2}{30}\cdot 100=37.3\%\]

Tortilla Chips:

\[\frac{8.2}{30}\cdot 100=27.3\%\]

Pretzels:

\[\frac{4.3}{30}\cdot 100=14.3\%\]

Popcorn:

\[\frac{3.8}{30}\cdot 100=12.7\%\]

Snack Nuts:

\[\frac{2.5}{30}\cdot 100=8.3\%\]

---

Step 3: With a protractor and a compass draw the graph using the appropriate degree measures.

---

To see this done watch the following video: